pH分配仮説

膜透過と薬物の形

分子形薬物は膜を透過することができるが、イオン形薬物はできない。
このことを踏まえてpH変化と酸性・塩基性薬物について考えていく。

pH変化と酸性薬物

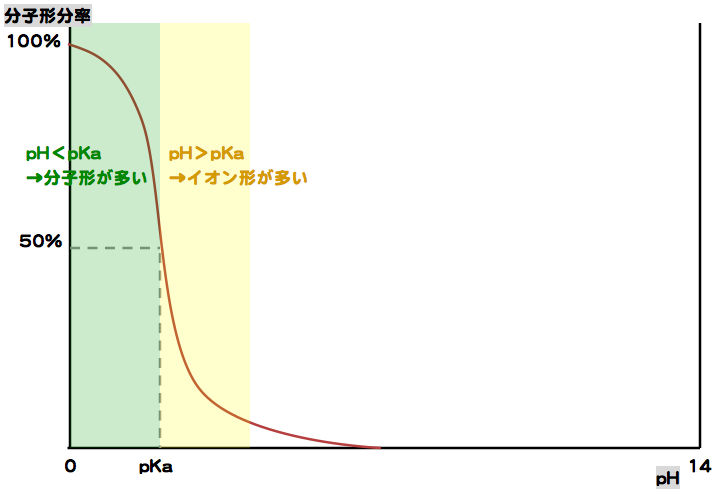
酸性薬物では、pH ＞ pKaのときイオン形が多くなり、pH ＜ pKaのとき分子形が多くなる。

また、pKaの異なる酸性薬物のグラフを組み合わせると次のようになる。

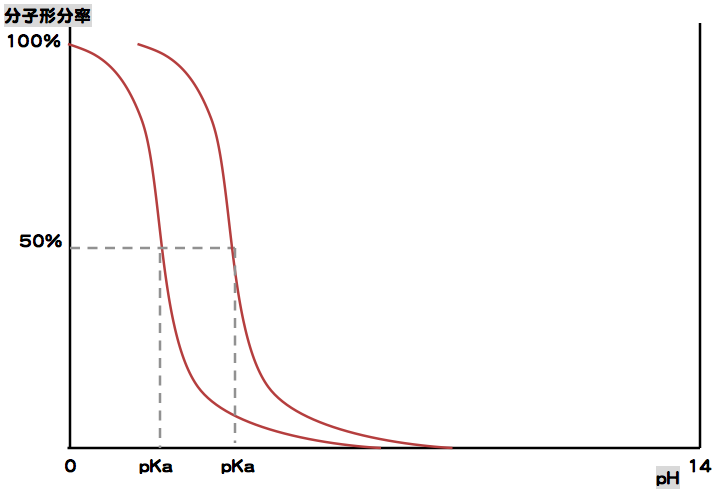
グラフを見てわかるように、pKaの大きい薬物の方が分子形が存在する割合が大きくなるので、効率よく吸収できる。（分子量が同程度の場合）

pH変化と塩基性薬物

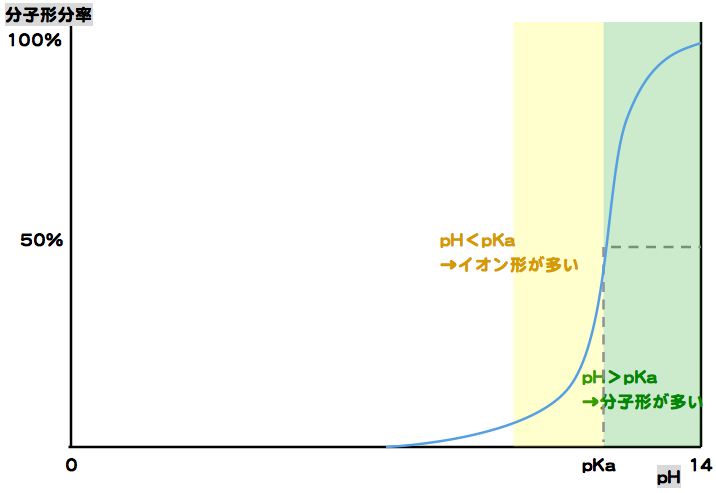
塩基性薬物では、pH ＞ pKaのとき分子形が多くなり、pH ＜ pKaのときイオン形が多くなる。

また、pKaが異なる２つの塩基性薬物のグラフを組み合わせると以下のようになる。

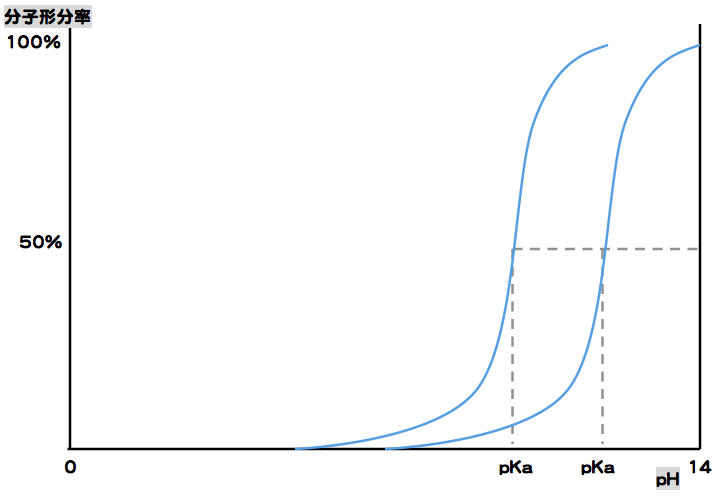
グラフから、pKaが小さい方が分子形の割合が多くなり、従って吸収もいいということが判断できる。

pH分配仮説とヘンダーソン・ハッセルバルヒの式

POINT

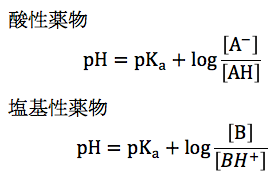
薬物のpH・pKa・分子形/イオン形比の関係は、上の式で表すことができる。
実際にこの式を用いて以下の問題を解いてみる。

アスピリンは酸性薬物なので、pH=pKa+log（［A–］/［HA］）に値を当てはめる。

以上より、アスピリンは胃内でほとんどが分子形として存在しているので、溶けにくいと判断できる。